Comparison with pymatgen#
The pymatgen project also has tools capable of calculating the mean-squared displacement and diffusion coefficient from a relevant input. So why should you use kinisi over pymatgen?
The simple answer is that the approach taken by kinisi, which is outlined in the methodology, uses a higher precision approach to estimate the diffusion coefficent and offers an accurate estimate in the variance of the mean-squared displacements and diffusion coefficient from a single simulation.
In this notebook, we will compare the results from pymatgen and kinisi. First we will import the kinisi and pymatgen DiffusionAnalyzer classes.
[1]:
import numpy as np
from kinisi.analyze import DiffusionAnalyzer as KinisiDiffusionAnalyzer
from pymatgen.analysis.diffusion.analyzer import DiffusionAnalyzer as PymatgenDiffusionAnalyzer
from pymatgen.io.vasp import Xdatcar
np.random.seed(42)
The kinisi.DiffusionAnalyzer API was based on the pymatgen equivalent, therefore, the two take the same inputs and can parse the Xdatcar.structures.
[2]:
p_params = {'specie': 'Li',
'time_step': 2.0,
'step_skip': 50}
[3]:
xd = Xdatcar('./example_XDATCAR.gz')
We can then run both the pymagten analysis and the kinisi analysis (the pymatgen requires and additional temperature keyword which is not used in this example).
[4]:
pymatgen_diff = PymatgenDiffusionAnalyzer.from_structures(
xd.structures, temperature=300, **p_params)
[5]:
kinisi_diff = KinisiDiffusionAnalyzer.from_pymatgen(
xd.structures, parser_params=p_params)
- Reading Trajectory: 0%| | 0/140 [00:00<?, ?it/s]
</pre>
- Reading Trajectory: 0%| | 0/140 [00:00<?, ?it/s]
end{sphinxVerbatim}
Reading Trajectory: 0%| | 0/140 [00:00<?, ?it/s]
- Reading Trajectory: 100%|██████████| 140/140 [00:00<00:00, 4626.48it/s]
</pre>
- Reading Trajectory: 100%|██████████| 140/140 [00:00<00:00, 4626.48it/s]
end{sphinxVerbatim}
Reading Trajectory: 100%|██████████| 140/140 [00:00<00:00, 4626.48it/s]
- Getting Displacements: 0%| | 0/100 [00:00<?, ?it/s]
</pre>
- Getting Displacements: 0%| | 0/100 [00:00<?, ?it/s]
end{sphinxVerbatim}
Getting Displacements: 0%| | 0/100 [00:00<?, ?it/s]
- Getting Displacements: 100%|██████████| 100/100 [00:00<00:00, 16168.63it/s]
</pre>
- Getting Displacements: 100%|██████████| 100/100 [00:00<00:00, 16168.63it/s]
end{sphinxVerbatim}
Getting Displacements: 100%|██████████| 100/100 [00:00<00:00, 16168.63it/s]
- Finding Means and Variances: 0%| | 0/100 [00:00<?, ?it/s]
</pre>
- Finding Means and Variances: 0%| | 0/100 [00:00<?, ?it/s]
end{sphinxVerbatim}
Finding Means and Variances: 0%| | 0/100 [00:00<?, ?it/s]
- Finding Means and Variances: 15%|█▌ | 15/100 [00:00<00:00, 149.67it/s]
</pre>
- Finding Means and Variances: 15%|█▌ | 15/100 [00:00<00:00, 149.67it/s]
end{sphinxVerbatim}
Finding Means and Variances: 15%|█▌ | 15/100 [00:00<00:00, 149.67it/s]
- Finding Means and Variances: 31%|███ | 31/100 [00:00<00:00, 150.57it/s]
</pre>
- Finding Means and Variances: 31%|███ | 31/100 [00:00<00:00, 150.57it/s]
end{sphinxVerbatim}
Finding Means and Variances: 31%|███ | 31/100 [00:00<00:00, 150.57it/s]
- Finding Means and Variances: 47%|████▋ | 47/100 [00:00<00:00, 154.23it/s]
</pre>
- Finding Means and Variances: 47%|████▋ | 47/100 [00:00<00:00, 154.23it/s]
end{sphinxVerbatim}
Finding Means and Variances: 47%|████▋ | 47/100 [00:00<00:00, 154.23it/s]
- Finding Means and Variances: 64%|██████▍ | 64/100 [00:00<00:00, 159.91it/s]
</pre>
- Finding Means and Variances: 64%|██████▍ | 64/100 [00:00<00:00, 159.91it/s]
end{sphinxVerbatim}
Finding Means and Variances: 64%|██████▍ | 64/100 [00:00<00:00, 159.91it/s]
- Finding Means and Variances: 82%|████████▏ | 82/100 [00:00<00:00, 167.00it/s]
</pre>
- Finding Means and Variances: 82%|████████▏ | 82/100 [00:00<00:00, 167.00it/s]
end{sphinxVerbatim}
Finding Means and Variances: 82%|████████▏ | 82/100 [00:00<00:00, 167.00it/s]
- Finding Means and Variances: 100%|██████████| 100/100 [00:00<00:00, 178.30it/s]
</pre>
- Finding Means and Variances: 100%|██████████| 100/100 [00:00<00:00, 178.30it/s]
end{sphinxVerbatim}
Finding Means and Variances: 100%|██████████| 100/100 [00:00<00:00, 178.30it/s]
Now we can plot the mean-squared displacement from each to check agreement, the pymatgen time units are femtoseconds so these are adjusted.
[6]:
import matplotlib.pyplot as plt
[7]:
plt.plot(pymatgen_diff.dt / 1000, pymatgen_diff.msd, label='pymatgen')
plt.plot(kinisi_diff.dt, kinisi_diff.msd, label='kinisi')
plt.legend()
plt.ylabel('MSD/Å$^2$')
plt.xlabel('$\Delta t$/ps')
plt.show()
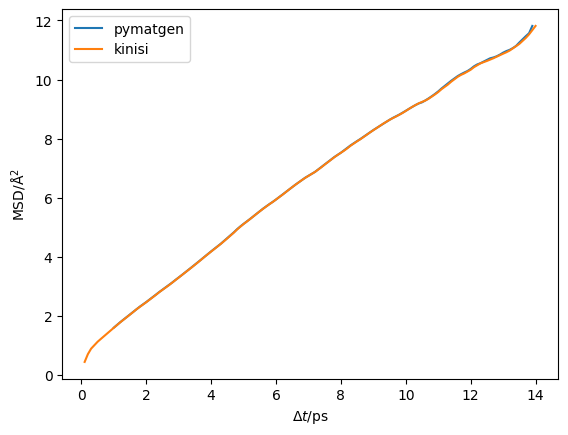
We can see that the results overlap almost entirely.
However, this doesn’t show the benefits for using kinisi over pymatgen. The first benefit is that kinisi will accurately estimate the variance in the observed mean-squared displacements, giving error bars for the above plot.
[8]:
plt.errorbar(kinisi_diff.dt, kinisi_diff.msd, kinisi_diff.msd_std, c='#ff7f0e')
plt.ylabel('MSD/Å$^2$')
plt.xlabel('$\Delta t$/ps')
plt.show()
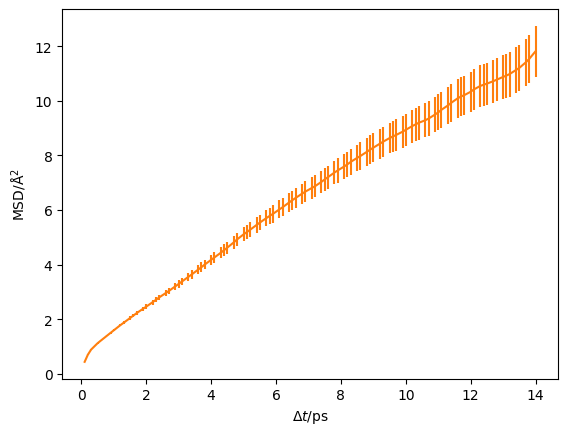
The second benefit is that kinisi will estimate the diffusion coefficient with an accurate uncertainty. pymatgen also estimates this uncertainty, however, pymatgen assumes that the data is independent and applies weighted least squares. However, mean-squared displacement observations are inherently dependent (as discussed in the thought experiment in the
methodology), so kinisi accounts for this and applied a generalised least squares style approach. This means that the estimated variance in the diffusion coefficient from kinisi is accurate (while, pymatgen will heavily underestimate the value) and given the
BLUE nature of the GLS approach, kinisi has a higher probability of determining a value for the diffusion coefficient closer to the true diffusion coefficient.
[9]:
kinisi_diff.diffusion(kinisi_diff.ngp_max)
- Likelihood Sampling: 0%| | 0/1500 [00:00<?, ?it/s]
</pre>
- Likelihood Sampling: 0%| | 0/1500 [00:00<?, ?it/s]
end{sphinxVerbatim}
Likelihood Sampling: 0%| | 0/1500 [00:00<?, ?it/s]
- Likelihood Sampling: 4%|▍ | 58/1500 [00:00<00:02, 578.49it/s]
</pre>
- Likelihood Sampling: 4%|▍ | 58/1500 [00:00<00:02, 578.49it/s]
end{sphinxVerbatim}
Likelihood Sampling: 4%|▍ | 58/1500 [00:00<00:02, 578.49it/s]
- Likelihood Sampling: 12%|█▏ | 177/1500 [00:00<00:01, 936.85it/s]
</pre>
- Likelihood Sampling: 12%|█▏ | 177/1500 [00:00<00:01, 936.85it/s]
end{sphinxVerbatim}
Likelihood Sampling: 12%|█▏ | 177/1500 [00:00<00:01, 936.85it/s]
- Likelihood Sampling: 20%|█▉ | 297/1500 [00:00<00:01, 1051.81it/s]
</pre>
- Likelihood Sampling: 20%|█▉ | 297/1500 [00:00<00:01, 1051.81it/s]
end{sphinxVerbatim}
Likelihood Sampling: 20%|█▉ | 297/1500 [00:00<00:01, 1051.81it/s]
- Likelihood Sampling: 28%|██▊ | 415/1500 [00:00<00:00, 1102.20it/s]
</pre>
- Likelihood Sampling: 28%|██▊ | 415/1500 [00:00<00:00, 1102.20it/s]
end{sphinxVerbatim}
Likelihood Sampling: 28%|██▊ | 415/1500 [00:00<00:00, 1102.20it/s]
- Likelihood Sampling: 36%|███▌ | 534/1500 [00:00<00:00, 1131.49it/s]
</pre>
- Likelihood Sampling: 36%|███▌ | 534/1500 [00:00<00:00, 1131.49it/s]
end{sphinxVerbatim}
Likelihood Sampling: 36%|███▌ | 534/1500 [00:00<00:00, 1131.49it/s]
- Likelihood Sampling: 43%|████▎ | 652/1500 [00:00<00:00, 1147.74it/s]
</pre>
- Likelihood Sampling: 43%|████▎ | 652/1500 [00:00<00:00, 1147.74it/s]
end{sphinxVerbatim}
Likelihood Sampling: 43%|████▎ | 652/1500 [00:00<00:00, 1147.74it/s]
- Likelihood Sampling: 51%|█████▏ | 772/1500 [00:00<00:00, 1163.47it/s]
</pre>
- Likelihood Sampling: 51%|█████▏ | 772/1500 [00:00<00:00, 1163.47it/s]
end{sphinxVerbatim}
Likelihood Sampling: 51%|█████▏ | 772/1500 [00:00<00:00, 1163.47it/s]
- Likelihood Sampling: 59%|█████▉ | 892/1500 [00:00<00:00, 1174.67it/s]
</pre>
- Likelihood Sampling: 59%|█████▉ | 892/1500 [00:00<00:00, 1174.67it/s]
end{sphinxVerbatim}
Likelihood Sampling: 59%|█████▉ | 892/1500 [00:00<00:00, 1174.67it/s]
- Likelihood Sampling: 67%|██████▋ | 1011/1500 [00:00<00:00, 1179.26it/s]
</pre>
- Likelihood Sampling: 67%|██████▋ | 1011/1500 [00:00<00:00, 1179.26it/s]
end{sphinxVerbatim}
Likelihood Sampling: 67%|██████▋ | 1011/1500 [00:00<00:00, 1179.26it/s]
- Likelihood Sampling: 75%|███████▌ | 1131/1500 [00:01<00:00, 1185.42it/s]
</pre>
- Likelihood Sampling: 75%|███████▌ | 1131/1500 [00:01<00:00, 1185.42it/s]
end{sphinxVerbatim}
Likelihood Sampling: 75%|███████▌ | 1131/1500 [00:01<00:00, 1185.42it/s]
- Likelihood Sampling: 83%|████████▎ | 1251/1500 [00:01<00:00, 1189.10it/s]
</pre>
- Likelihood Sampling: 83%|████████▎ | 1251/1500 [00:01<00:00, 1189.10it/s]
end{sphinxVerbatim}
Likelihood Sampling: 83%|████████▎ | 1251/1500 [00:01<00:00, 1189.10it/s]
- Likelihood Sampling: 91%|█████████▏| 1372/1500 [00:01<00:00, 1192.81it/s]
</pre>
- Likelihood Sampling: 91%|█████████▏| 1372/1500 [00:01<00:00, 1192.81it/s]
end{sphinxVerbatim}
Likelihood Sampling: 91%|█████████▏| 1372/1500 [00:01<00:00, 1192.81it/s]
- Likelihood Sampling: 99%|█████████▉| 1492/1500 [00:01<00:00, 1194.77it/s]
</pre>
- Likelihood Sampling: 99%|█████████▉| 1492/1500 [00:01<00:00, 1194.77it/s]
end{sphinxVerbatim}
Likelihood Sampling: 99%|█████████▉| 1492/1500 [00:01<00:00, 1194.77it/s]
- Likelihood Sampling: 100%|██████████| 1500/1500 [00:01<00:00, 1143.36it/s]
</pre>
- Likelihood Sampling: 100%|██████████| 1500/1500 [00:01<00:00, 1143.36it/s]
end{sphinxVerbatim}
Likelihood Sampling: 100%|██████████| 1500/1500 [00:01<00:00, 1143.36it/s]
[10]:
from uncertainties import ufloat
[11]:
print('D from pymatgen:',
ufloat(pymatgen_diff.diffusivity, pymatgen_diff.diffusivity_std_dev))
D from pymatgen: (1.33307+/-0.00008)e-05
[12]:
print('D from kinisi:',
ufloat(np.mean(kinisi_diff.D), np.std(kinisi_diff.D, ddof=1)))
D from kinisi: (1.53+/-0.07)e-05
The comparison between weighted and generalised least squared estimators will be discussed in full in a future publication covering the methodology of kinisi.